2025年广东公需课学习指引及答案
截止时间为2026年4月30日
微信:15816122881 | QQ:444161476
围绕国家和省委省政府经济社会高质量发展的部署要求,结合我省继续教育工作实际,经研究和论证,我省2025年度专业技术人员继续教育公需科目确定为“人工智能赋能制造业高质量发展”、“新质生产力与现代化产业体系”两个专题。
2️⃣ 学习任务
2025年度全省专业技术人员继续教育公需科目学习任务按30学时计算,专业技术人员从2个专题中任意选择1个学满30学时,均可认定为完成当年度的公需科目学习任务。
3️⃣ 学习途径
更新于 2021.06.25 21:00
广东省教师继续教育信息管理平台:https://jsglpt.gdedu.gov.cn/
咨询电话:400-998-9352 ( 帐号与密码说明 | 客服 | 留言)
广东省卫生健康行业学习平台网址:https://www.91huayi.com
咨询电话: 020-38914613(华医网)
4️⃣ 教师资格证书定期注册学时要求
连续五年,每年累计应不少于90学时,其中公需课不少于30学时,专业课不少于42学时,选修课不少于18学时。
5️⃣ 学习结果




6️⃣ 考核答案
💠人工智能赋能制造业高质量发展
💠新质生产力与现代化产业体系
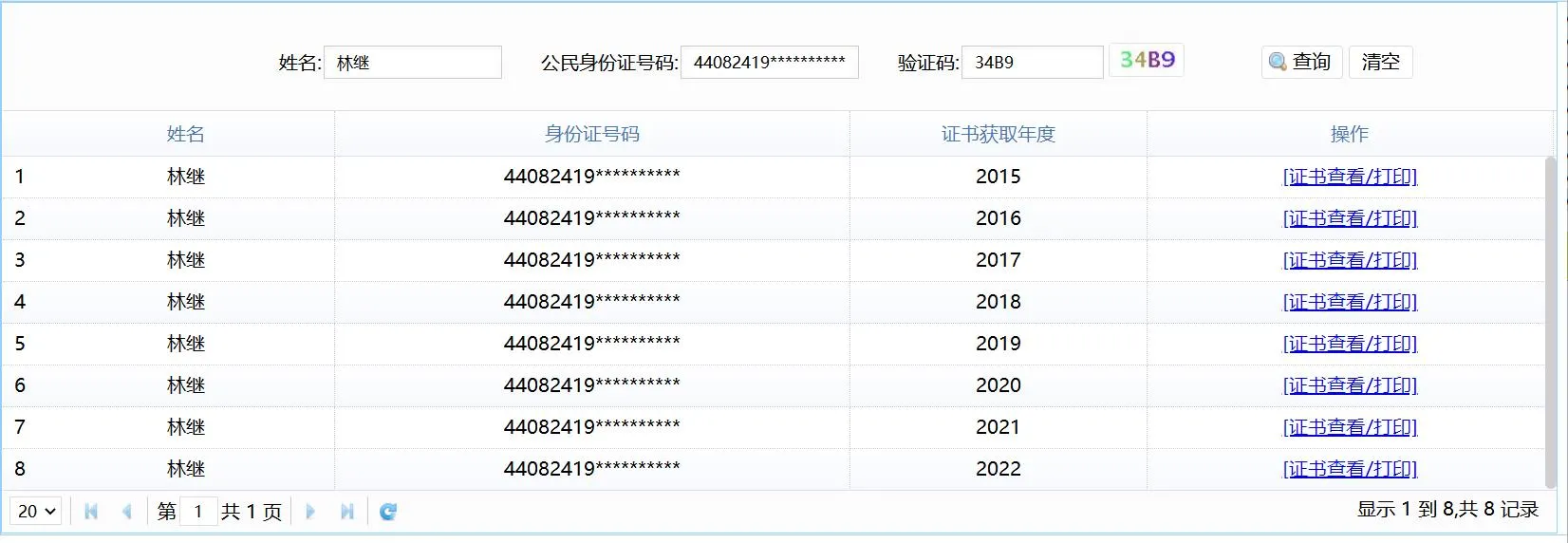
7️⃣ 学时查询、证书打印查询学时(专业课、选修课、公需课):省教师继教平台=广东省教师继续教育信息管理平台
查询学时(专业课、选修课、公需课)、打印继续教育证书:广东省人力资源和社会保障厅网上服务平台
注:专技网平台=广东省专业技术人员继续教育管理系统
打印专业技术人员继续教育证书
 8️⃣ 公需课代挂说明
8️⃣ 公需课代挂说明1、我这边都是通过真实浏览器进行网课代挂,一般都是 1 倍速进行播放(特殊要求除外)。可以保证学习记录不异常,学时正常记录。
2、我崇尚的理念是:一次合作,终身合作。有代挂需求的人基本上都是体系内的公职人员,年年都要学网课,最害怕学习出现问题(如倍速/秒过后学时异常被通报批评,无法获取本年度学分等),我这边都是真实浏览器代挂,不倍速,不秒过,积累老客户,做回头客生意。
3、收费标准:每位20元。
4、需要帮忙的老师可以在赞赏码留言栏填写帐号与密码。

继续教育 2020-04-18 20:10:24 通过 网页 浏览(7000511) 打印


共有10条评论!
谢谢您的答案!
谢谢您的答案,辛苦了!
谢谢您的答案,辛苦了!
专业课和选修课在德诚选择吗?
林继回复:在德诚平台可以报名学习专业课和选修课。只是第一批学习已经在4月底终止,不知道第二批什么时候开始报名学习。
谢谢亲贡献的答案
感谢您的答案!
谢谢你的答案
谢谢你的答案
谢谢你的答案
谢谢您的答案